LLaMA微调显存需求减半，清华提出4比特优化器

站长网2023-09-08 18:15:500阅

大模型的训练和微调对显存要求很高，优化器状态是显存主要开销之一。近日，清华大学朱军、陈键飞团队提出了用于神经网络训练的4比特优化器，节省了模型训练的内存开销，同时能达到与全精度优化器相当的准确率。

4比特优化器在众多预训练和微调任务上进行了实验，在保持准确率无损的情况下可将微调 LLaMA-7B 的显存开销降低多达57%。

论文:https://arxiv.org/abs/2309.01507

代码:https://github.com/thu-ml/low-bit-optimizers

模型训练的内存瓶颈

从 GPT-3，Gopher 到 LLaMA，大模型有更好的性能已成为业界的共识。但相比之下，单个 GPU 的显存大小却增长缓慢，这让显存成为了大模型训练的主要瓶颈，如何在有限的 GPU 内存下训练大模型成为了一个重要的难题。

为此，我们首先需要明确消耗显存的来源有哪些。事实上来源有三类，分别是:

1. 「数据显存」，包括输入的数据和神经网络每层输出的激活值，它的大小直接受到 batch size 以及图像分辨率 / 上下文长度的影响;

2. 「模型显存」，包括模型参数，梯度，以及优化器状态（optimizer states），它的大小与模型参数数量呈正比;

3. 「临时显存」，包括 GPU kernel 计算时用到的临时内存和其他缓存等。随着模型规模的增大，模型显存的占比逐渐增大，成为主要瓶颈。

优化器状态的大小由使用哪种优化器决定。当前，训练 Transformer 往往使用 AdamW 优化器，它们在训练过程中需要存储并更新两个优化器状态，即一阶和二阶矩（first and second moments）。如果模型参数量为 N，那么 AdamW 中优化器状态的数量为2N，这显然是一笔极大的显存开销。

以 LLaMA-7B 为例，该模型含的参数数量大约7B，如果使用全精度（32比特）的 AdamW 优化器对它进行微调，那么优化器状态所占用的显存大小约为52.2GB。此外，虽然朴素的 SGD 优化器不需要额外状态，节省了优化器状态所占用的内存，但是模型的性能难以保证。因此，本文主要关注如何减少模型内存中的优化器状态，同时保证优化器的性能不受损。

节省优化器内存的方法

目前在训练算法方面，节省优化器显存开销的方法主要有三类:

1. 通过低秩分解（Factorization）的思路对优化器状态进行低秩近似(low-rank approximation);

2. 通过只训练一小部分参数来避免保存大多数的优化器状态，例如 LoRA;

3. 基于压缩（compression）的方法，使用低精度数值格式来表示优化器状态。

特别的，Dettmers et al. （ICLR2022）针对 SGD with momentum 和 AdamW 提出了相应的8比特优化器，通过使用分块量化(block-wise quantization)和动态指数数值格式(dynamic exponential numerical format)的技术，在语言建模、图像分类、自监督学习、机器翻译等任务上达到了与原有的全精度优化器相匹配的效果。

本文在基础上，将优化器状态的数值精度进一步降低至4比特，提出了针对不同优化器状态的量化方法，最终提出了4比特 AdamW 优化器。同时，本文探索了将压缩和低秩分解方法结合的可能性，提出了4比特 Factor 优化器，这种混合式的优化器同时享有好的性能和更好的内存高效性。本文在众多经典的任务上对4比特优化器进行了评估，包括自然语言理解、图像分类、机器翻译和大模型的指令微调。

在所有的任务上，4比特优化器达到了与全精度优化器可比的效果，同时能够占用更少的内存。

问题设置

基于压缩的内存高效优化器的框架

首先，我们需要了解如何将压缩操作引入到通常使用的优化器中，这由算法1给出。其中，A 是一个基于梯度的优化器（例如 SGD 或 AdamW）。该优化器输入现有的参数 w，梯度 g 和优化器状态 s，输出新的参数和优化器状态。在算法1中，全精度的 s_t 是暂时存在的，而低精度的 (s_t ) ̅ 会持久地保存在 GPU 内存中。这种方式能够节省显存的重要原因是:神经网络的参数往往由每层的参数向量拼接而成。因此，优化器更新也是逐层 / 张量进行，进而在算法1下，最多只有一个参数的优化器状态以全精度的形式留在内存中，其他层对应的优化器状态都处于被压缩的状态。

主要的压缩方法:量化（quantization）

量化是用低精度数值来表示高精度数据的技术，本文将量化的操作解耦为两部分:归一化（normalization）和映射(mapping)，从而能够更加轻量级的设计并实验新的量化方法。归一化和映射两个操作依次以逐元素的形式施加在全精度数据上。归一化负责将张量中的每个元素投射到单位区间，其中张量归一化(per-tensor normalization)和分块归一化(block-wise normalization)分别如下定义:

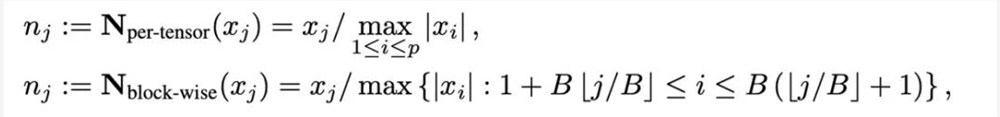
不同归一化方法的粒度不同，处理异常值的能力会有所区别，同时带来的额外内存开销也不同。而映射（mapping）操作负责将归一化的数值映射到低精度能够表示的整数。正式地讲，给定位宽 b(即量化后每个数值使用 b 比特来表示)和预先定义的函数 T

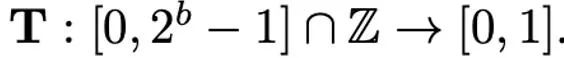
映射操作被定义为:

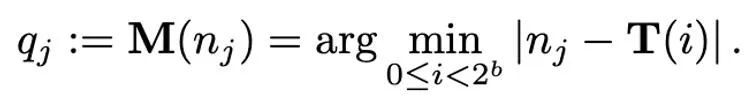
因此，如何设计恰当的 T 对于减小量化误差有很重要的作用。本文主要考虑线性映射（linear）和动态指数映射(dynamic exponent)。最后，去量化的过程就是按顺序施加映射（mapping）和归一化(normalization)的逆算子。

一阶矩的压缩方法

以下主要针对 AdamW 的优化器状态（一阶矩和二阶矩）提出不同的量化方法。对于一阶矩，本文的量化方法主要基于 Dettmers et al. (ICLR2022)的方法，使用分块归一化(块大小为2048)和动态指数映射。

在初步的实验中，我们直接将位宽从8比特降低至4比特，发现一阶矩对于量化十分鲁棒，在很多任务上已经达到匹配的效果，但也在一部分任务上出现性能上的损失。为了进一步提高性能，我们仔细研究了一阶矩的模式，发现在单个张量中存在很多异常值。

此前的工作对于参数和激活值的异常值的模式已有一定的研究，参数的分布较为平滑，而激活值则具有按照 channel 分布的特点。本文发现，优化器状态中异常值的分布较为复杂，其中有些张量的异常值分布在固定的行，而另外一些张量的异常值分布在固定的列。

对于异常值按列分布的张量，以行为优先的分块归一化可能会遇到困难。因此，本文提出采用更小的块，块大小为128，这能够在减小量化误差的同时使额外的内存开销保持在可控的范围内。下图展示了不同块大小的量化误差。

二阶矩的压缩方法

与一阶矩相比，二阶矩的量化更加困难并且会带来训练的不稳定性。本文确定了零点问题是量化二阶矩的主要瓶颈，此外针对病态的异常值分布提出了改进的归一化方法:rank-1normalization。本文也尝试了对二阶矩的分解方法（factorization）。

零点问题

在参数、激活值、梯度的量化中，零点往往是不可缺少的，并且在也是量化后频率最高的点。但是，在 Adam 的迭代公式中，更新的大小正比于二阶矩的 -1/2次方，因此在零附近的范围内改变会极大影响更新的大小，进而造成不稳定。

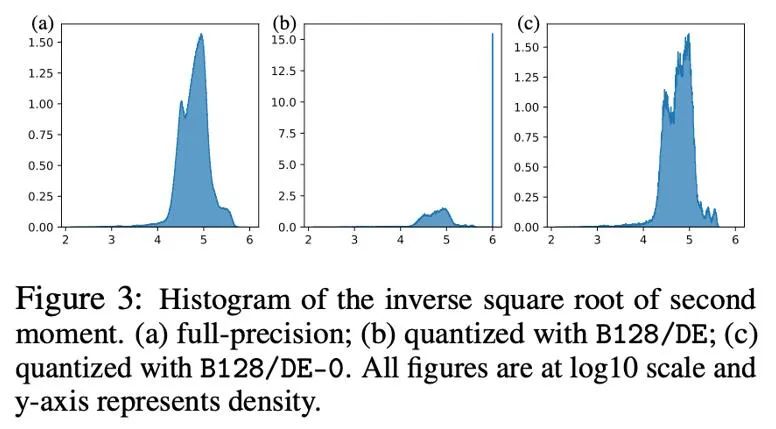
下图以直方图的形式展示了量化前后 Adam 二阶矩 -1/2次方的分布，即 h （v）=1/(√v 10^(-6) )。如果将零点包括在内(图 b)，那么大多数值都被推到了10^6，从而导致极大的近似误差。一个简单的办法是在动态指数映射中将零点移除，在这样做之后(图 c)，对二阶矩的近似变得更加精确。在实际情况中，为了有效利用低精度数值的表达能力，我们提出采用移除零点的线性映射，在实验中取得了很好的效果。

Rank-1归一化

基于一阶矩和二阶矩复杂的异常值分布，并受 SM3优化器所启发，本文提出了一种新的归一化方法，命名为 rank-1归一化。对一个非负的矩阵张量 x∈R^（n×m），它的一维统计量定义为:

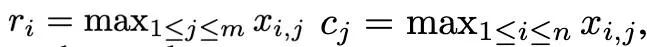
进而 rank-1归一化可以被定义为:

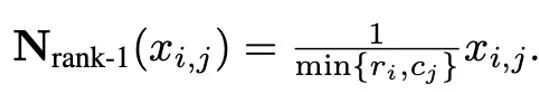
rank-1归一化以更细粒度的方式利用了张量的一维信息，能够更聪明且有效地处理按行分布或按列分布的异常值。此外，rank-1归一化能够简单的推广到高维张量中，并且随着张量规模的增大，它所产生的额外内存开销要小于分块归一化。

此外，本文发现 Adafactor 优化器中对于二阶矩的低秩分解方法能够有效的避免零点问题，因此也对低秩分解和量化方法的结合进行了探索。下图展示了针对二阶矩的一系列消融实验，证实了零点问题是量化二阶矩的瓶颈，同时也验证了 rank-1归一化，低秩分解方法的有效性。

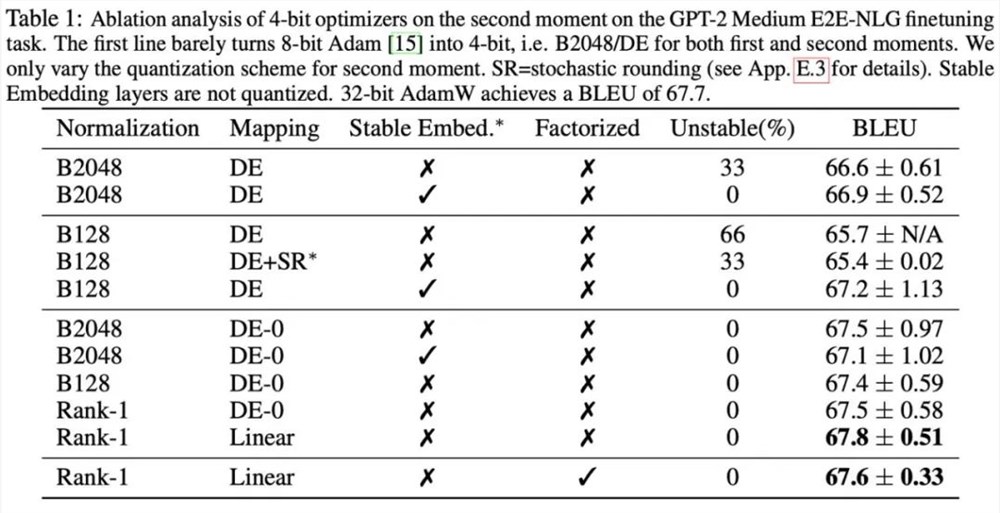
实验结果

研究根据所观察的现象和使用的方式，最终提出两种低精度优化器:4比特 AdamW 和4比特 Factor，并与其他优化器进行对比，包括8比特 AdamW，Adafactor， SM3。研究选择在广泛的任务上进行评估，包括自然语言理解、图像分类、机器翻译和大模型的指令微调。下表展示了各优化器在不同任务上的表现。

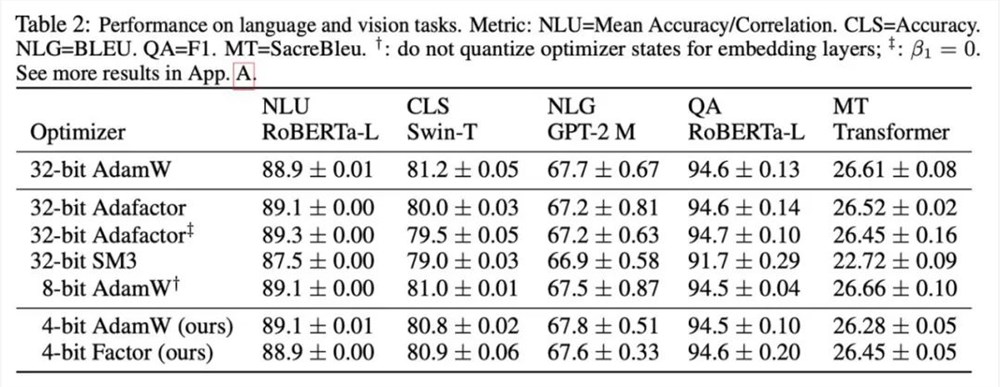
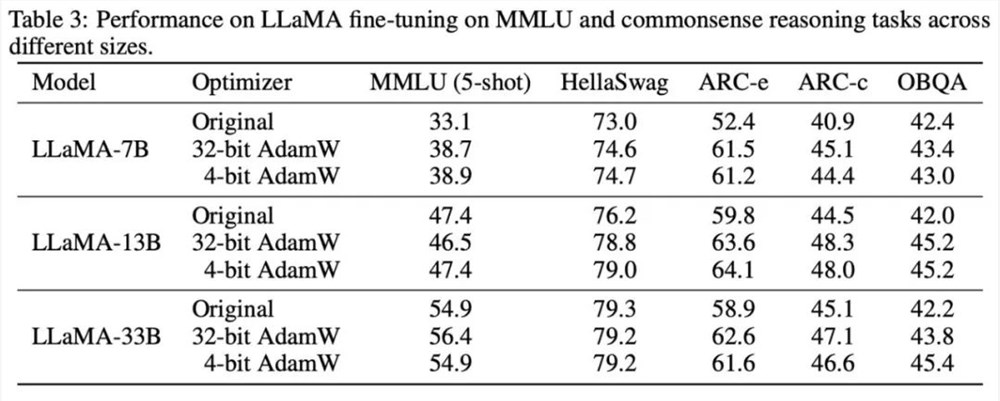
可以看到，在所有的微调任务上，包括 NLU，QA，NLG，4比特优化器可以匹配甚至超过32比特 AdamW，同时在所有的预训练任务上，CLS，MT，4比特优化器达到与全精度可比的水平。从指令微调的任务中可以看到，4比特 AdamW 并不会破坏预训练模型的能力，同时能较好地使它们获得遵守指令的能力。

之后，我们测试了4比特优化器的内存和计算效率，结果如下表所示。相比8比特优化器，本文提出的4比特优化器能够节省更多内存，在 LLaMA-7B 微调的实验中最高节省57.7%。此外，我们提供了4比特 AdamW 的融合算子版本，它能够在节省内存的同时不影响计算效率。对于 LLaMA-7B 的指令微调任务，由于缓存压力减小，4比特 AdamW 也为训练带来了加速效果。详细的实验设置和结果可参考论文链接。