GPT-4 MATH准确率最高涨至84.3%!港中文、清华等七所顶尖高校提出全新CSV方法
【新智元导读】让模型用代码自我验证解决方案,结合多数投票集成机制,推理准确率可以提升近30%!
虽然大型语言模型(LLMs)在常识理解、代码生成等任务中都取得了非常大的进展,不过在数学推理任务上仍然存在很大改进空间,经常会生成无意义、不准确的内容,或是无法处理过于复杂的计算。
最近推出的一些语言模型,如GPT-4, PaLM-2都在数学推理上取得了重大进步,特别是OpenAI的最新版模型GPT-4Code Interpreter,在较困难的数学推理数据集上也展现出了很高的性能。

为了探索「代码生成任务」对「语言模型推理能力」的影响,来自香港中文大学、南京大学、中国科学技术大学、清华大学、香港城市大学、长沙理工大学和塔夫茨大学的研究人员联合发布了一篇论文,通过在代码使用频率(Code Usage Frequency)上引入不同的约束限制进行实验验证。

论文链接:https://arxiv.org/abs/2308.07921
实验结果显示,GPT-4Code Interpreter模型的成功在很大程度上要归功于「在生成和执行代码、评估代码执行的输出以及在收到不合理的输出」时纠正其解决方案方面的强大能力。
基于上述结论,研究人员提出了一种新颖且高效的提示方法,显式的基于代码的自我验证(CSV, code-based self-verification),以进一步提高GPT-4代码解释器的数学推理潜力。
该方法在GPT-4Code Interpreter上采用zero-shot提示,以促使模型使用代码来对答案进行自我验证。
在验证状态为「假」的情况下,模型将自动修改其解决方案,类似于人类在数学考试中纠错的过程。
此外,研究人员还发现验证结果的状态可以指示解决方案的置信度,并进一步提高多数表决的有效性。
通过结合GPT-4Code Interpreter和CSV方法,在MATH数据集上的零样本准确率实现了从54.9%到84.3%的巨大提升。
为了探索代码的使用对GPT4-Code解决数学问题能力的影响,研究人员采用了一种很直接的方法,即通过精心设计的提示来限制GPT4-Code与代码的交互。
具体包括两种代码限制提示以及一种基础提示用来对比:

提示1:No code usage is allowed(不允许使用代码)
GPT4-Code不允许在其解决方案中添加代码,也就是说模型只能完全依赖自然语言(NL)推理链,类似于思维链(CoT)框架中的解决方案,由此产生的推理步骤序列叫做CNL,如上图中(a)所示。
提示2:Code can be used only once(代码只能使用一次)
GPT4-Code只能用单个代码块内的代码来生成解决方案,类似于之前的PAL方法,论文中将此序列称为CSL,即使用符号语言(SL),如Python进行推理,上图中(b)为样例。
基本提示:对代码使用没有任何限制。
推理序列可表示为
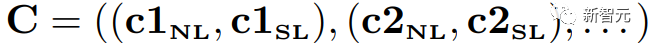
,其中每个步骤都由自然语言和 Python 代码组成,示例如上图中(c)所示。
除此之外,研究人员还引入了代码使用频率(Code Usage Frequency)来记录不同提示下的代码执行次数,结果表明,GPT4-Code的高性能与高代码使用频率之间存在正相关。
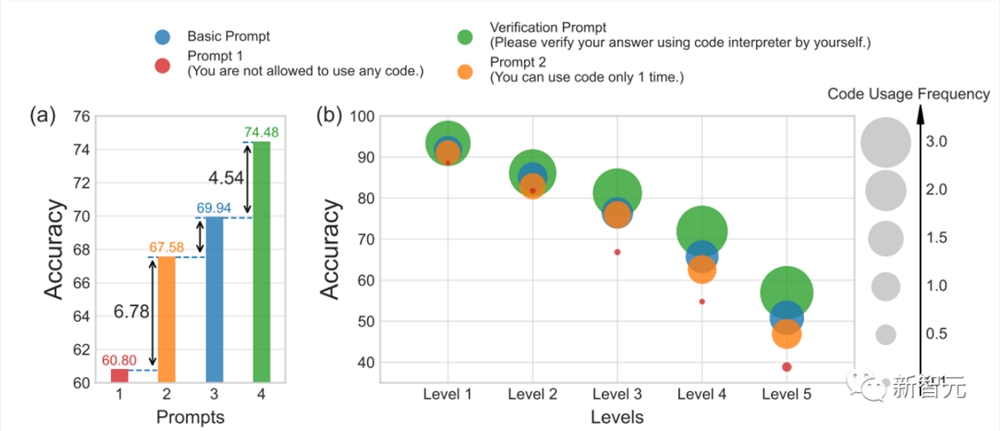
具体来说,提示2使用的代码量比提示1多了一倍,并且提示2比提示1的准确率提高了6.9%,表明Python代码链CSL比自然语言链CNL更能提高计算能力,这一观察结果与之前基于Python的提示方法结果一致。
不过只能使用一次代码也存在缺陷,当代码输出引发错误或产生非预期的结果时,模型缺乏自我调试(self-debugging)的能力。
在对比提示2和基本提示时,可以发现,基本提示始终能生成包含多个代码使用实例的解决方案,即代码使用频率更高,并且基本提示的准确性也明显提高。
具体可以归因于代码的两个优势:
1. 生成一些简短的代码块,可以分割自然语言推理步骤,从而带来更高的准确率;
2. 模型有能力评估代码执行结果,并在结果中发现错误或不合逻辑的解决步骤,并进行修正。
受代码使用频率分析观察结果的启发,研究人员决定利用GPT4-Code的代码生成、代码评估、代码执行,以及自动调整解决方案等能力来增强方案验证,以提高推理性能。
CSV的主要流程就是对GPT-Code输入提示,来显式地通过代码生成来验证答案正确性。
对解决方案C的验证结果V可以分为「真」、「假」、「不确定」三类。
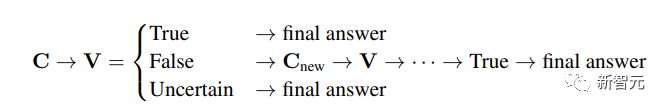
与CSV结合后,模型能够使用代码来验证答案,然后在验证结果为「错误」的情况下审查并调整得出解决方案的方式,从而获得正确答案。

在完善和修正初始解决方案后,准确率可以得到显著提高。
值得注意的是,验证(verification)和修正(rectification)阶段都是基于代码的,所以必然会导致代码使用频率的增加。
在 GPT4-Code 出现之前,先前的框架大多依赖于外部LLM使用自然语言进行验证和精心设计的少样本提示。
相比之下,CSV方法仅依赖于GPT4-Code的直接提示,以零样本的方式简化了流程,利用其先进的代码执行机制来自主验证和独立修正解决方案。
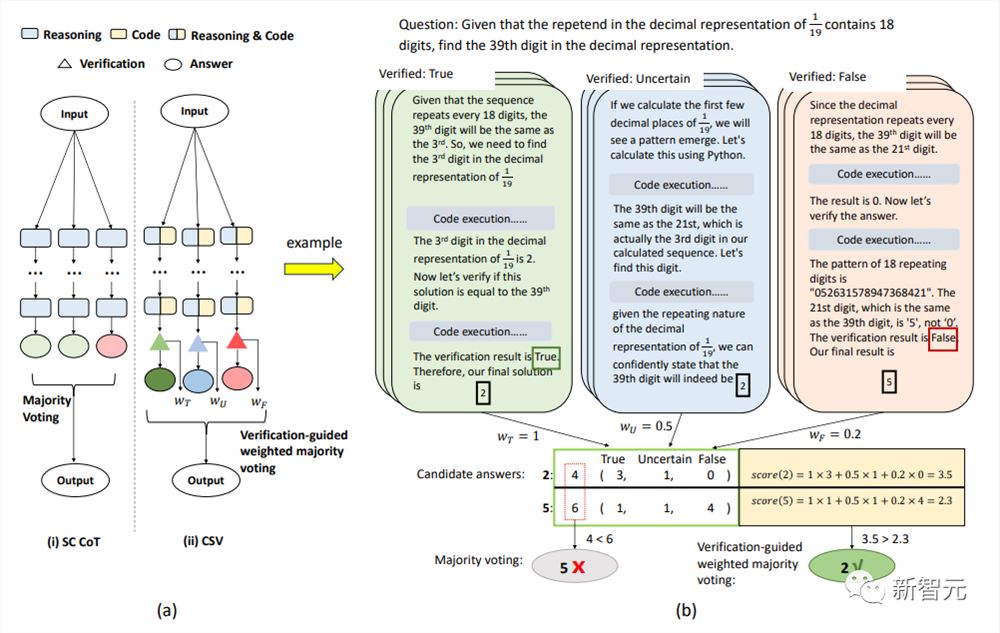
研究人员还将验证阶段集成到了加权多数表决(majority voting)中,为验证过程的各个状态分配了不同的权重。
为了防止答案被确认为「假」后不再进行其他验证,研究人员将三种状态分配了不同的权重:wT, wF和wU,可以增加系统的可靠性。
为了简单起见,集成算法从k个解决方案中提取一对最终答案及其相应的验证结果,表示为
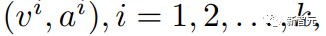
其中v和a分别代表第i个最终答案和最终验证结果。
因此,每个候选答案 a 的投票得分可以表示为:
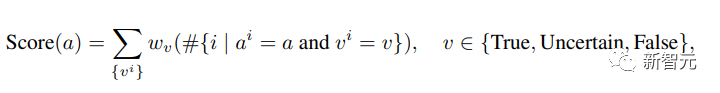
最后从所有候选答案中选出得分最高的答案:
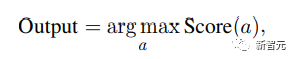
MATH数据集
GPT4-Code在MATH基准上的准确率达到了69.69%,大大超过了之前的方法(53.90%),表明 GPT4-Code在解决数学问题方面表现出很强的能力。
在GPT4-Code的基础上,文中提出的CSV方法进一步提高了准确性,将准确率提高到了73.54%;
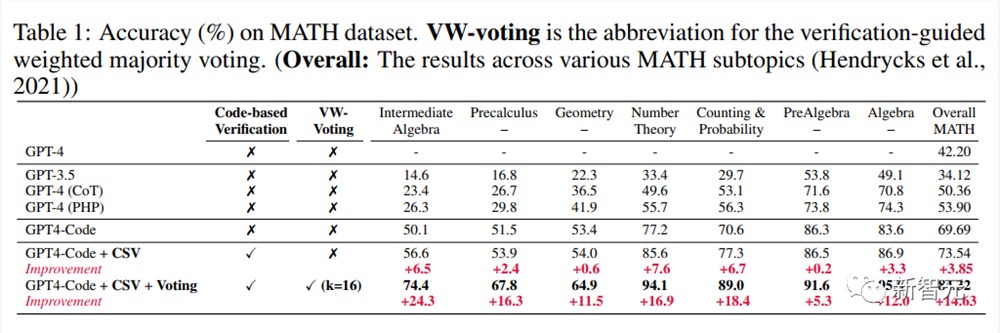
在加入基于代码的显式自我验证和验证引导的加权多数投票(采样路径数为16)后,结果进一步提高到了84.32%
需要注意的是,虽然增加基于代码的自我验证可以提高题目的成绩,但具体程度因题目难度、形式而异。
其他数据集
研究人员还在其他推理数据集上应用了CSV方法,包括GSM8K、MMLU-Math 和 MMLU-STEM
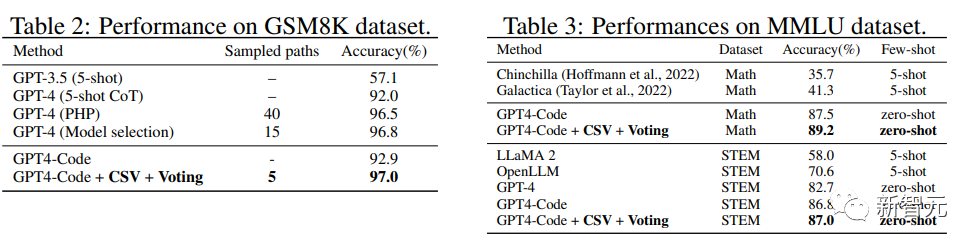
从结果上来看,CSV GPT4-Code在各个数据集上都取得了最优的结果。
与带有模型选择功能的GPT-4和 PHP相比,验证引导的多数表决是减少采样路径数量的有效框架。
CSV方法与现有模型在MMLU-Math和MMLU-STEM数据集上的性能对比中,可以看到开源模型明显优于闭源模型。
为了弥补这一差距,研究人员表示目前已经开始着手准备制作数据集,并将在不久的将来公开发布。
其他开源LLM模型,如LLaMA2可以利用该数据集进行微调,并进一步提升数学推理能力。
参考资料:
https://arxiv.org/abs/2308.07921
- 0000
- 0001
- 0000
- 0000
- 0000


