谷歌:大模型不仅有涌现能力,训练时间长了还有「领悟」能力
模型在达到一定规模时会出现涌现现象,谷歌的研究表明,模型在训练到一定时间后,会出现另一种现象,即「领悟」现象。
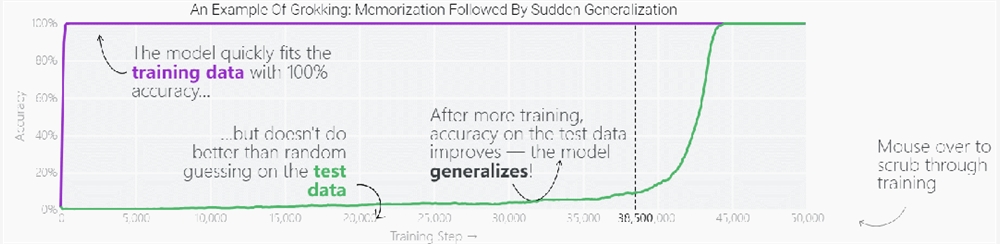
2021年,研究人员在训练一系列微型模型时取得了一个惊人的发现,即模型经过长时间的训练后,会有一个变化,从开始只会「记忆训练数据」,转变为对没见过的数据也表现出很强的泛化能力。
这种现象被称为「领悟(grokking)」,如下图所示,模型在长时间拟合训练数据后,「领悟」现象会突然出现。
既然微型模型有这种特性,那么更复杂一点的模型在经过更长时间的训练后,是否也会突然出现「领悟」现象?最近大型语言模型(LLM)发展迅猛,它们看起来对世界有着丰富的理解力,很多人认为 LLM 只是在重复所记忆的训练内容,这一说法正确性如何,我们该如何判断 LLM 是输出记忆内容,还是对输入数据进行了很好的泛化?
为了更好的了解这一问题,本文来自谷歌的研究者撰写了一篇博客,试图弄清楚大模型突然出现「领悟」现象的真正原因。

本文先从微型模型的训练动态开始,他们设计了一个具有24个神经元的单层 MLP,训练它们学会做模加法(modular addition)任务,我们只需知道这个任务的输出是周期性的,其形式为 (a b) mod n。
MLP 模型权重如下图所示,研究发现模型的权重最初非常嘈杂,但随着时间的增加,开始表现出周期性。

如果将单个神经元的权重可视化,这种周期性变化更加明显:
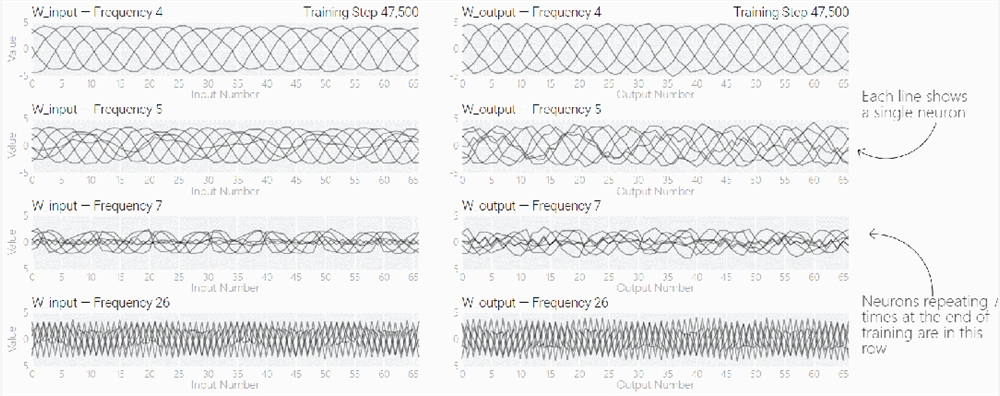
别小看周期性,权重的周期性表明该模型正在学习某种数学结构,这也是模型从记忆数据转变为具有泛化能力的关键。很多人对这一转变感到迷惑,为什么模型会从记忆数据模式转变为泛化数据模式。
用01序列进行实验
为了判断模型是在泛化还是记忆,该研究训练模型预测30个1和0随机序列的前三位数字中是否有奇数个1。例如000110010110001010111001001011为0,而010110010110001010111001001011为1。这基本就是一个稍微棘手的 XOR 运算问题,带有一些干扰噪声。如果模型在泛化,那么应该只使用序列的前三位数字;而如果模型正在记忆训练数据,那么它还会使用后续数字。
该研究使用的模型是一个单层 MLP,在1200个序列的固定批上进行训练。起初,只有训练准确率有所提高,即模型会记住训练数据。与模运算一样,测试准确率本质上是随机的,随着模型学会通用解决方案而急剧上升。
通过01序列问题这个简单的示例,我们可以更容易地理解为什么会发生这种情况。原因就是模型在训练期间会做两件事:最小化损失 和权重衰减。在模型泛化之前,训练损失实际上会略有增加,因为它交换了与输出正确标签相关的损失,以获得较低的权重。
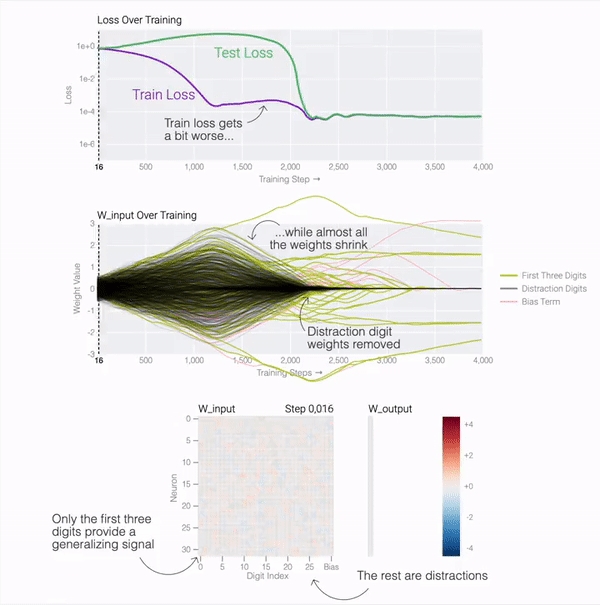
测试损失的急剧下降使得模型看起来像是突然泛化,但如果查看模型在训练过程中的权重,大多数模型都会在两个解之间平滑地插值。当与后续分散注意力的数字相连的最后一个权重通过权重衰减被修剪时,快速泛化就会发生。
「领悟」现象是什么时候发生的?
值得注意的是,「领悟(grokking)」是一种偶然现象 —— 如果模型大小、权重衰减、数据大小和其他超参数不合适,「领悟」现象就会消失。如果权重衰减太少,模型就会对训练数据过渡拟合。如果权重衰减过多,模型将无法学到任何东西。
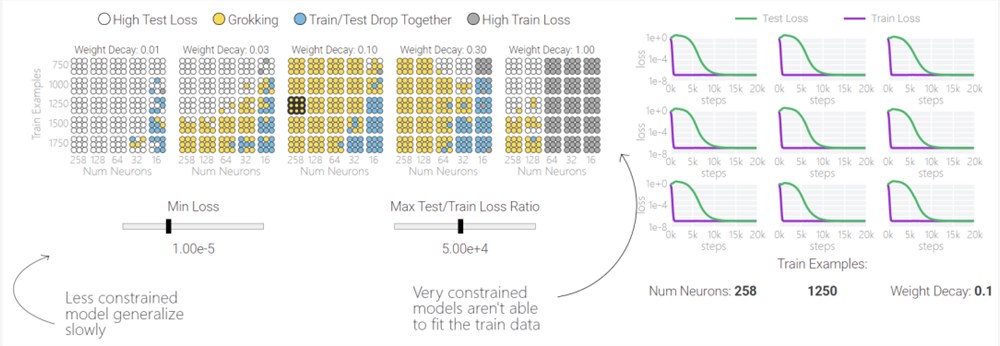
下面,该研究使用不同的超参数针对1和0任务训练了1000多个模型。训练过程充满噪音,因此针对每组超参数训练了九个模型。表明只有两类模型出现「领悟」现象,蓝色和黄色。
具有五个神经元的模块化加法
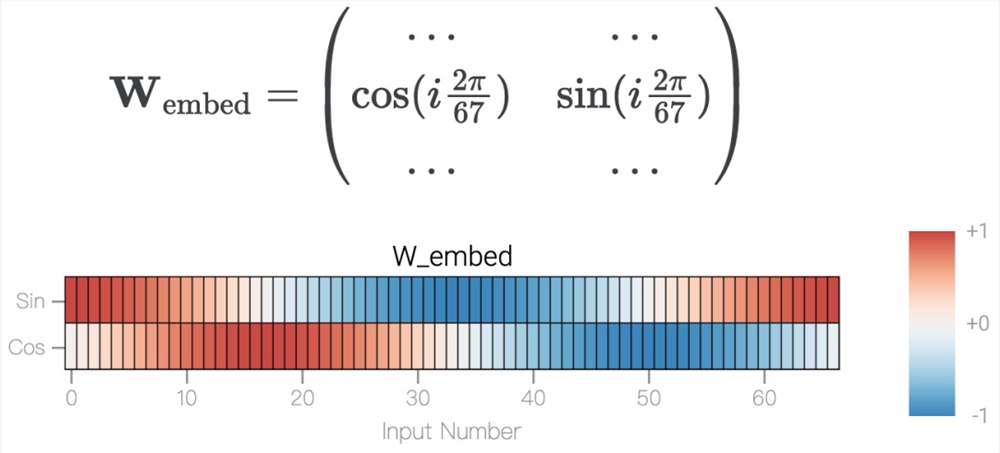
模加法 a b mod67是周期性的,如果总和超过67,则答案会产生环绕现象,可以用一个圆来表示。为了简化问题,该研究构建了一个嵌入矩阵,使用 cos 和 sin 将 a 和 b 放置在圆上,表示为如下形式。
结果表明,模型仅用5个神经元就可以完美准确地找到解决方案:

观察经过训练的参数,研究团队发现所有神经元都收敛到大致相等的范数。如果直接绘制它们的 cos 和 sin 分量,它们基本上均匀分布在一个圆上。
接下来是
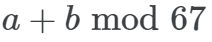
,它是从头开始训练的,没有内置周期性,这个模型有很多不同的频率。


该研究使用离散傅立叶变换 (DFT) 分离出频率。就像在1和0任务中一样,只有几个权重起到关键作用:
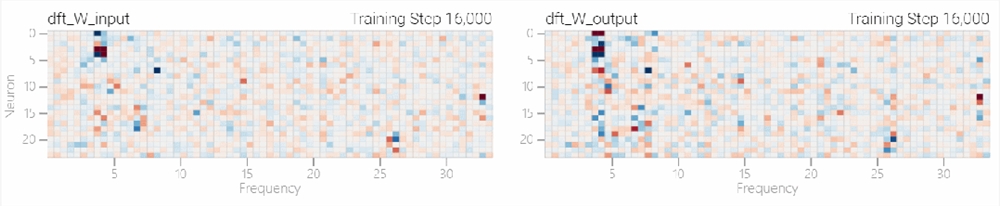
下图表明,在不同的频率,模型也能实现「领悟」:

开放问题
现在,虽然我们对单层 MLP 解决模加法的机制及其在训练过程中出现的原因有了扎实的了解,但在记忆和泛化方面仍有许多有趣的开放性问题。
哪种模型的约束效果更好呢?
从广义上讲,权重衰减的确可以引导各种模型避免记忆训练数据。其他有助于避免过拟合的技术包括 dropout、缩小模型,甚至数值不稳定的优化算法。这些方法以复杂的非线性方式相互作用,因此很难先验地预测哪种方法最终会诱导泛化。
此外,不同的超参数也会使改进不那么突然。
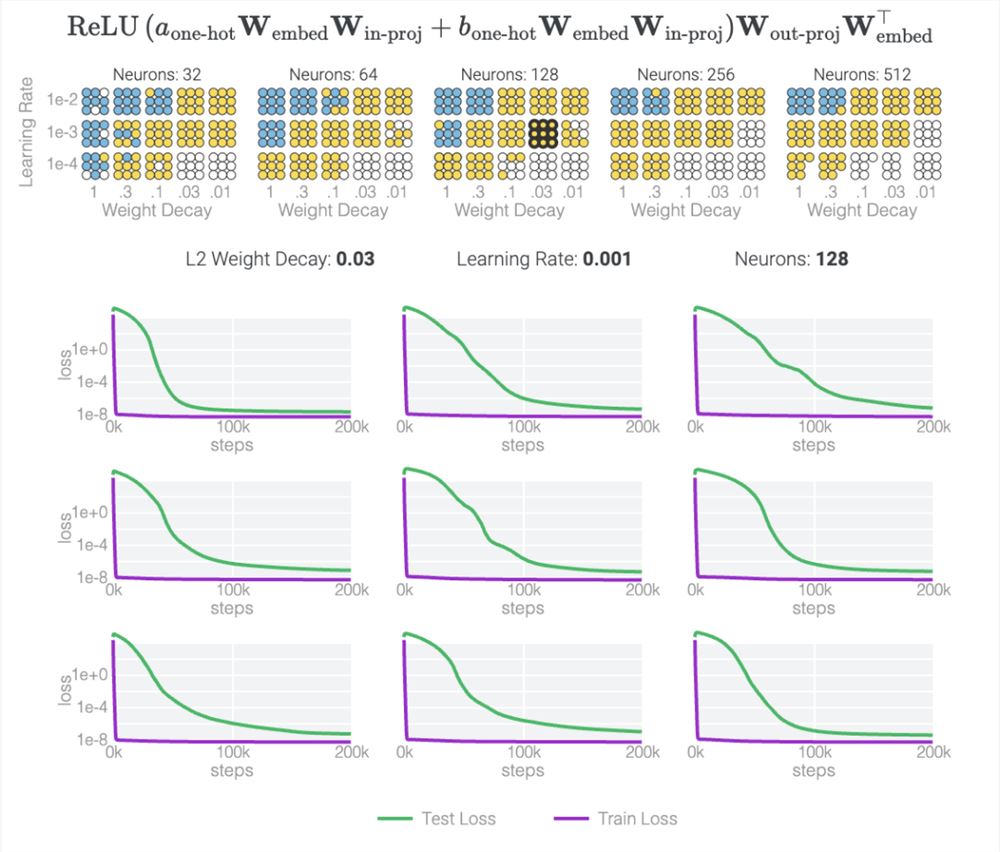
为什么记忆比泛化更容易?
有一种理论认为:记忆训练集的方法可能比泛化解法多得多。因此,从统计学上讲,记忆应该更有可能首先发生,尤其是在没有正则化或正则化很少的情况中。正则化技术(如权重衰减)会优先考虑某些解决方案,例如,优先考虑 「稀疏 」解决方案,而不是 「密集 」解决方案。
研究表明,泛化与结构良好的表征有关。然而,这不是必要条件;在求解模加法时,一些没有对称输入的 MLP 变体学习到的 「循环 」表征较少。研究团队还发现,结构良好的表征并不是泛化的充分条件。这个小模型(训练时没有权重衰减)开始泛化,然后转为使用周期性嵌入的记忆。
在下图中可以看到,如果没有权重衰减,记忆模型可以学习更大的权重来减少损失。
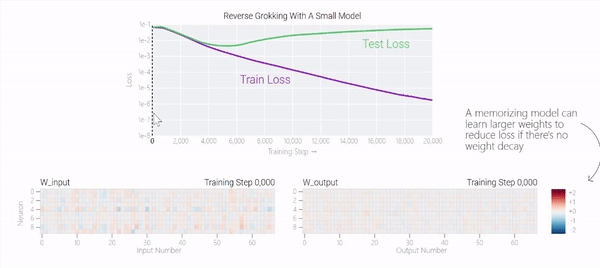
甚至可以找到模型开始泛化的超参数,然后切换到记忆,然后切换回泛化。
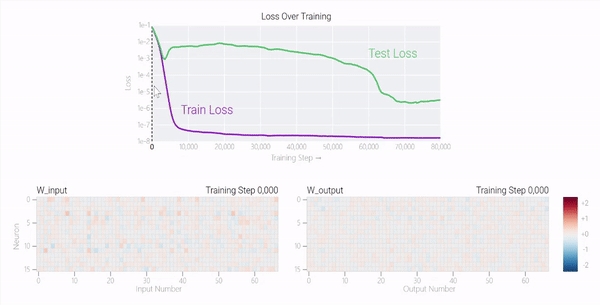
较大的模型呢?
理解模加法的解决方案并非易事。我们有希望理解更大的模型吗?在这条路上可能需要:
1) 训练更简单的模型,具有更多的归纳偏差和更少的运动部件。
2) 使用它们来解释更大模型如何工作的费解部分。
3) 按需重复。
研究团队相信,这可能是一种更好地有效理解大型模型的的方法,此外,随着时间的推移,这种机制化的可解释性方法可能有助于识别模式,从而使神经网络所学算法的揭示变得容易甚至自动化。
- 0001
- 0006
- 0000
- 0000
- 0000