古希腊这个几何问题,看着平淡无奇,却让一代代数学家绞尽脑汁

人们常用‘大海捞针’,‘煎水作冰’ ,‘化圆为方’等成语表示不可能完成的事情。这其中,‘化圆为方’蕴含着丰富的数学知识与数学思想,你知道是什么吗?此外,为什么‘化圆为方’就意味着不可能呢?数学家们又是如何证明其不可能性的呢?下面让我们一起来探究这个有趣的问题。
“化圆为方”最早由古希腊学者阿那克萨哥拉提出,他生活在公元前 5 世纪,在数学和哲学领域都有所贡献。相传他因亵渎神灵被捕入狱,在狱中实在过于无聊,便提出了这么一个作死问题:"怎样作出一个正方形,才能使它的面积与某个已知圆的面积相等?" 这就是化圆为方问题。之所以说这个问题作死,是因为阿那克萨哥拉虽然提出了这个问题,却不能提供参考答案,并且在这之后的 2400 多年里,无数大神们在这个问题上折戟沉沙,铩羽而归。
 ▲ 阿那克萨哥拉, 前 500 年 - 前 428 年(图自维基)
▲ 阿那克萨哥拉, 前 500 年 - 前 428 年(图自维基)
化圆为方是典型的尺规作图问题。所谓尺规作图(Compass-and-straightedge),就是只准许使用不带任何刻度的直尺和圆规绘制目标图形。 这种苛刻的作图条件使得原本很简单的几何作图中产生了一批著名的数学难题,化圆作方便是其中杰出代表。除此之外,还有三等分角问题和立方倍积问题,它们并列为尺规作图三大难题。
未来还会有另外文章介绍余下两个问题。
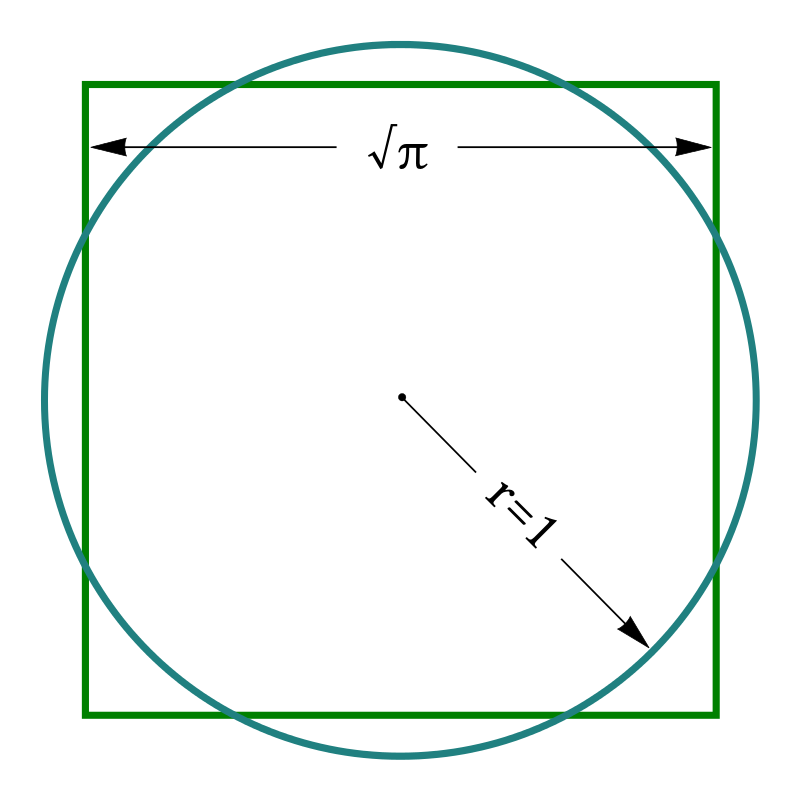 ▲ 化圆为方:求一正方形,其面积和一已知圆的面积相同(图自维基)
▲ 化圆为方:求一正方形,其面积和一已知圆的面积相同(图自维基)
在这里我们有必要先了解下尺规作图,在尺规作图中,直尺和圆规的定义是:
直尺:一侧为无穷长的直线,没有刻度也无法标识刻度的工具。只可以让笔摹下这个直线的全部或一部分。
圆规:由两端点构成的工具。可以在保持两个端点之间的距离不变的情况下,将两个端点同时移动,或者只固定其中一个端点,让另一个端点移动,作出圆弧或圆。两个端点之间的距离只能取已经作出的两点之间的距离,或者任意一个未知的距离。

定义了直尺和圆规的特性后,所有的作图步骤都可以归化为五种基本的步骤,称为作图公法(The basic constructions):
通过两个已知点,可以作出一直线。已知圆心和半径,可以作出一个圆。若两已知直线相交,能够确定其交点。若已知直线和一已知圆相交,能够确定其交点。若两已知圆相交,能够确定其交点。
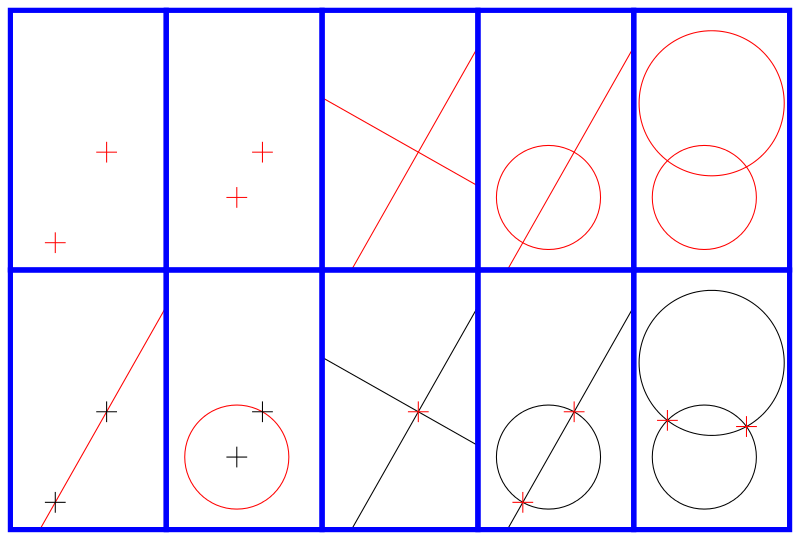 ▲ 作图公法的五种基本步骤
▲ 作图公法的五种基本步骤
尺规作图研究的,就是是否能够通过以上五种步骤的有限次重复,达到给定的作图目标。尺规作图问题常见的形式是:“给定某某条件,能否用尺规作出某某对象?”比如:“给定一个圆,能否用尺规作出这个圆的圆心?”,等等。
故有:化圆为方问题的完整叙述是: “给定一个圆,是否能够通过以上说明的五种基本步骤,于有限次内作出一个正方形,使得它的面积等于圆的面积”。
如果将圆的半径定为单位长度,则化圆为方问题的实质是作出长度为单位长度√π倍的线段。
要想证明化圆为方的不可能性,即要证明:在尺规作图的条件下,无法作出长度为单位长度√π 倍的线段,这等价于从 1 开始作出 π 。那么,是否可以做出呢?
结合我们所知情况,答案显然是不能。
因为能够用尺规作出的数 z 都有对应的最小多项式,即存在有理系数的多项式 m,使得 m(z)=0。
但对于圆周率 π 来说,这样的多项式不存在(由 1882 年林德曼等人证明)。所以无法用尺规作出数 z=π ,故化圆为方的不可能性得证。
数学上将类似于 这样没有对应的多项式的数称为超越数,有对应的多项式的数称为代数数。
上面关键之处在于林德曼等人的证明,他们用到了现在称为林德曼-魏尔斯特拉斯定理的结论。
虽然数学家们已经相互独立的证明了超越数不可能由尺规作图构造出来,但这并不影响人类天才解决问题的步伐。下面是一些独特的解法,受过启发的你能不能提出更好的想法呢?
根据前面所讲,化圆为方不可能性的本质在于 π 是超越数,如果将其转换为可用尺规作图方式作出的规矩数 z,就可以化不可能为可能,解决问题。
沿着这个思路,我们找到了“密率:355/113”,这一关键数。它由中国伟大数学家祖冲之最先发现,是一个与圆周率 π 非常近似且分子分母都是正整数的分数(也就是规矩数,属于代数数),可作出 π 的近似长度。
密率 ,是圆周率比较精确的一个分数近似值。出自《隋书·律历志上》:“密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。”
主要过程如下: 首先,转换形式:
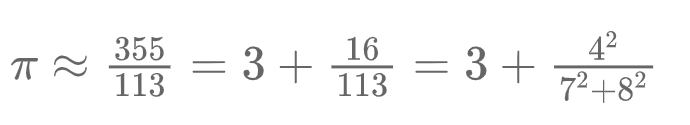
然后,我们注意到最右边分数,由四则运算和平方构成,符合尺规作图要求,所以我们可将其用尺规作图方法作出来。 尺规作图过程:

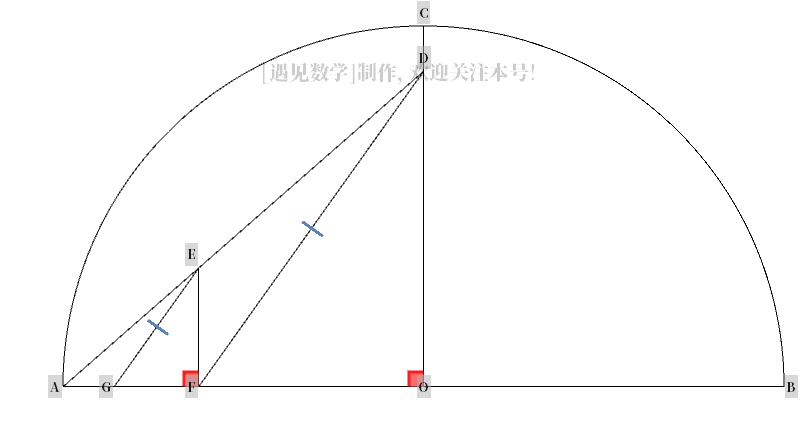
现在来论证目标线段 AG的长度: 由 △AEF ∽ △ADO 相似,得
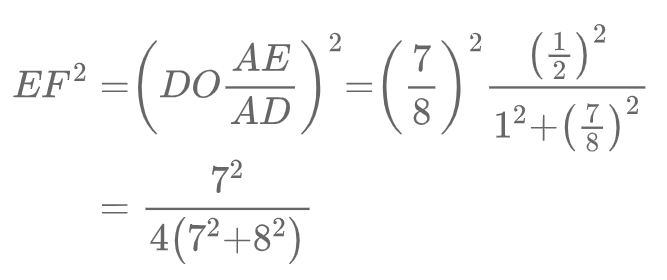
在 △AEF 中,有
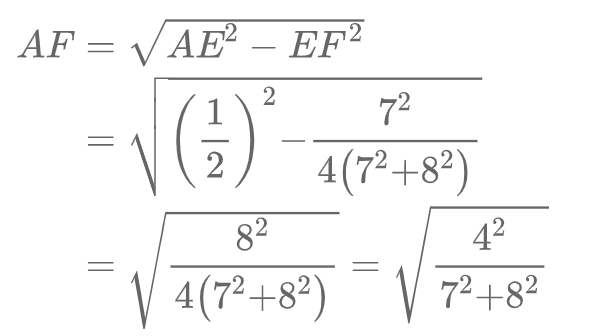
由 △AEG ∽ △ADF 相似,得
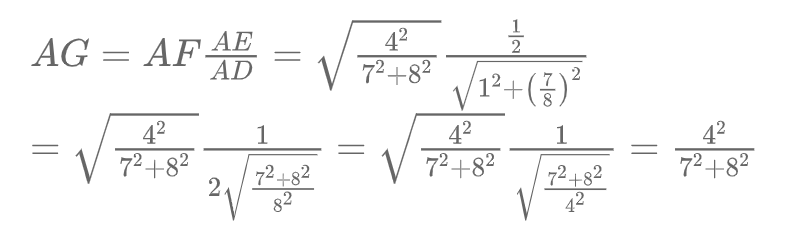

这样我们可以在一条直线上画出 AG 3AO 这么长的线段。如下图红线段所示:
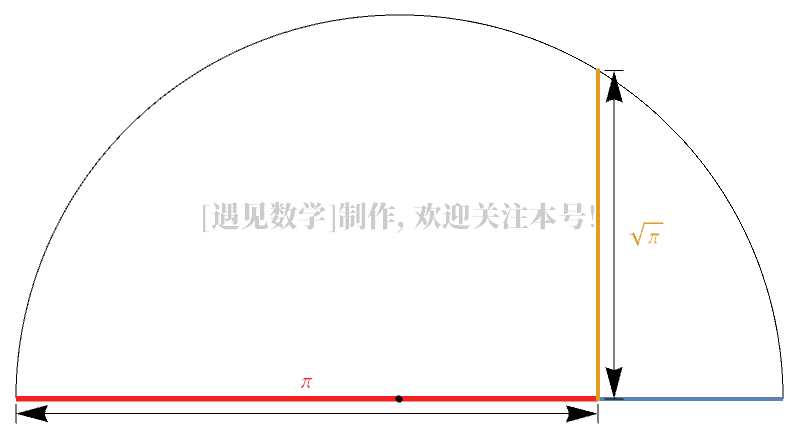
接下来我们要作出长度为 √π 的线段: 如上图所示,
再在长度为 的线段的右侧同一直线上接上一条长度为 1(也就是 AO)的线段以这两条线段的长度为直线作半圆过这两条线段的交界点作这两条线段的垂线(图中蓝色),与半圆相交根据相交弦定理,交点到直径的距离就为 √π 。
最后:我们就以这条垂线段为一边作正方形。这样,这个正方形的面积就极为近似地等于 π,即等于半径为 1 的圆的面积。 问题解决,利用密率,近似化圆为方!
上个解法是近似作图,毕竟 355/113 不真等于 π,现在我们跳出尺规作图这个框架,会发现思路开阔许多。
用已知圆为底,圆半径的 1/2 为高的圆柱,在平面上滚动一周,所得的矩形,其面积恰为圆的面积,如图:

证明:

最后,将所得矩形转化为等面积的正方形即可。
这样,化圆为方的问题得到了解决。这种方法由欧洲文艺复兴时期意大利数学家达芬奇提出,所以又称达芬奇解法。当然,这种解法虽然有新颖独特,极易理解等诸多优点,但问题也是存在的。首先是不精确,可操作性不强,所得结果误差较大。其次,违背了题设条件-尺规作图,用了直尺圆规以外的工具,这种开挂操作估计很难让人信服。不过这种从多方面多角度去看问题、分析问题和解决问题的思维方式还是很值得我们认真学习。
综上,想必大家对化圆为方问题已经有了大致了解。因为 π 为超越数,无法用尺规作图作出,所以化圆为方为一不可能事件。当然,这是建立在须用尺规作图的条件下,现代计算机借助代数工具已经可以完美地化圆为方,将不可能化为可能,解决了这个千年难题。
那么这几千年来无数英雄好汉前赴后继地研究这个不可能事件是不是就没有意义?显得太傻了呢?通过研究这些几何作图难题,而衍生发展出的尺规作图的判别准则,圆锥曲线研究,进而推动代数数和群论的方程论若干部分的发展,这些对数学发展产生了巨大影响的贡献成果显然不会同意这一观点。
同世间大多事一样,数学的迷人之处从不在于答案,而在于探索问题的过程,解决问题的方法,方法中蕴含的思想,思想里体现的深刻哲理。或许很多时候最后会发现如化圆为方一样是没有答案的,但细细品味整个思维过程产生的一些新思路、新方法和由此派生出的新哲理,你获得的这些早已超越了问题本身,不是吗?
本文作者:墨水(遇见数学核心成员),喜欢钻进书堆的傻猫一只,爱数学,爱运动,更爱喜欢数学的你们!
- 0000
- 0000
- 0000
- 0000
- 0000