预测token速度翻番!Transformer新解码算法火了,来自小羊驼团队
小羊驼团队的新研究火了。
他们开发了一种新的解码算法,可以让模型预测100个token数的速度提高1.5-2.3倍,进而加速LLM推理。
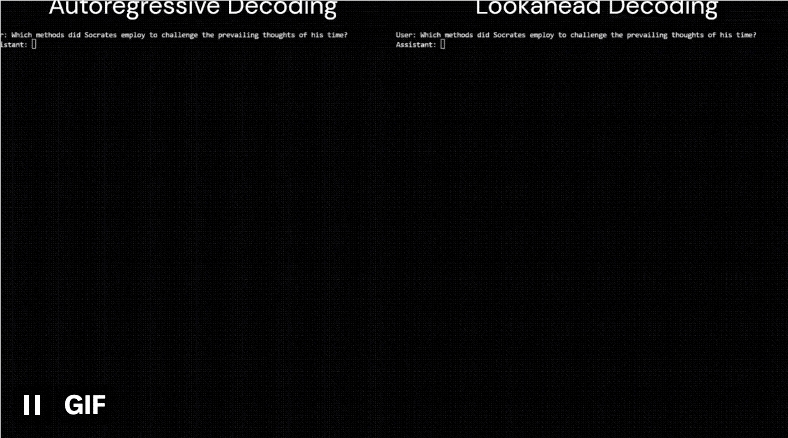
比如这是同一个模型(LLaMa-2-Chat7B)面对同一个用户提问(苏格拉底采用了哪些方法来挑战他那个时代的主流思想?)时输出回答的速度:
左边为原算法,耗时18.12s,每秒约35个token;
右边为该算法,耗时10.4s,每秒约60个token,明显快了一大截。
简单来说,这是一种并行解码算法,名叫“Lookahead Decoding”(前向解码)。
它主要利用雅可比(Jacobi)迭代法首次打破自回归解码中的顺序依赖性(众所周知,当下大模型基本都是基于自回归的Transformer)。
由此无需草稿模型(draft model)或数据存储,就可以减少解码步骤,加速LLM推理。
目前,作者已给出了与huggingface/transformers兼容的实现,只需几行代码,使用者即可轻松增强HF原生生成的性能。
有网友表示:
该方法实在有趣,没想到在离散设置上效果这么好。

还有人称,这让我们离“即时大模型”又近了一步。

具体如何实现?
加速自回归解码的重要性
不管是GPT-4还是LLaMA,当下的大模型都是基于自回归解码,这种方法下的推理速度其实是非常慢的。
因为每个自回归解码步骤一次仅生成一个token。
这样一来,模型输出的延迟有多高就取决于回答的长度。
更糟的是,这样的操作方式还浪费了现代GPU的并行处理能:GPU利用率都很低。
对于聊天机器人来说,当然是延迟越低,响应越快越好(尤其面对长序列答案时)。
此前,有人提出了一种叫做推测解码的加速自回归解码的算法,大致思路是采用猜测和验证策略,即先让草稿模型预测几个潜在的未来token,然后原始LLM去并行验证。
该方法可以“凭好运气”减少解码步骤的数量,从而降低延迟.
但也有不少问题,比如效果受到token接受率的限制,创建准确的草稿模型也麻烦,通常需要额外的训练和仔细的调整等。
在此,小羊驼团队提出了一种的新的精确并行解码算法,即前向解码来克服这些挑战。
前向解码打破顺序依赖性
前向解码之所以可行,是作者们观察到:
尽管一步解码多个新token是不可行的,但LLM确实可以并行生成多个不相交的n-grams——它们可能适合生成序列的未来部分。
这可以通过将自回归解码视为求解非线性方程,并采用经典的Jacobi迭代法进行并行解码来实现。
在过程中,我们就让生成的n-grams被捕获并随后进行验证,如果合适就将其集成到序列中,由此实现在不到n个步骤的时间内生成n个token的操作。
作者介绍,前向解码之所以能够“脱颖而出”,主要是因为它:
一不需草稿模型即可运行,简化了部署。
二是相对于每步 log(FLOPs)线性减少了解码步骤数,最终在单个GPU、不同数据集上实现快1.5倍-2.3倍的token数预测。
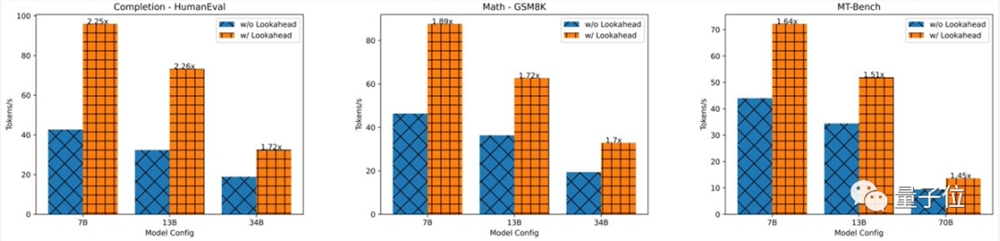
更重要的是,它允许分配更多(大于1个GPU)的 FLOP,以在对延迟极其敏感的应用程序中实现更大程度地延迟下降,尽管这会带来收益递减。
下面是具体介绍:
1、前向解码的动机Jacobi在进行求解非线性系统时,一并使用定点迭代方法一次性解码所有的未来token。
这个过程几乎看不到时钟加速。
2、前向解码通过收集和缓存Jacobi迭代轨迹生成的n-grams来利用Jacobi解码的能力。
下图为通过Jacobi解码收集2-grams,然后验证并加速解码的过程。
3、每个解码步骤有2个分支:
前向分支维护一个固定大小的2D窗口,以根据Jacobi轨迹生成n-grams;验证分支验证有希望的n-grams。
作者实现了二合一atten mask,以进一步利用GPU的并行计算能力。
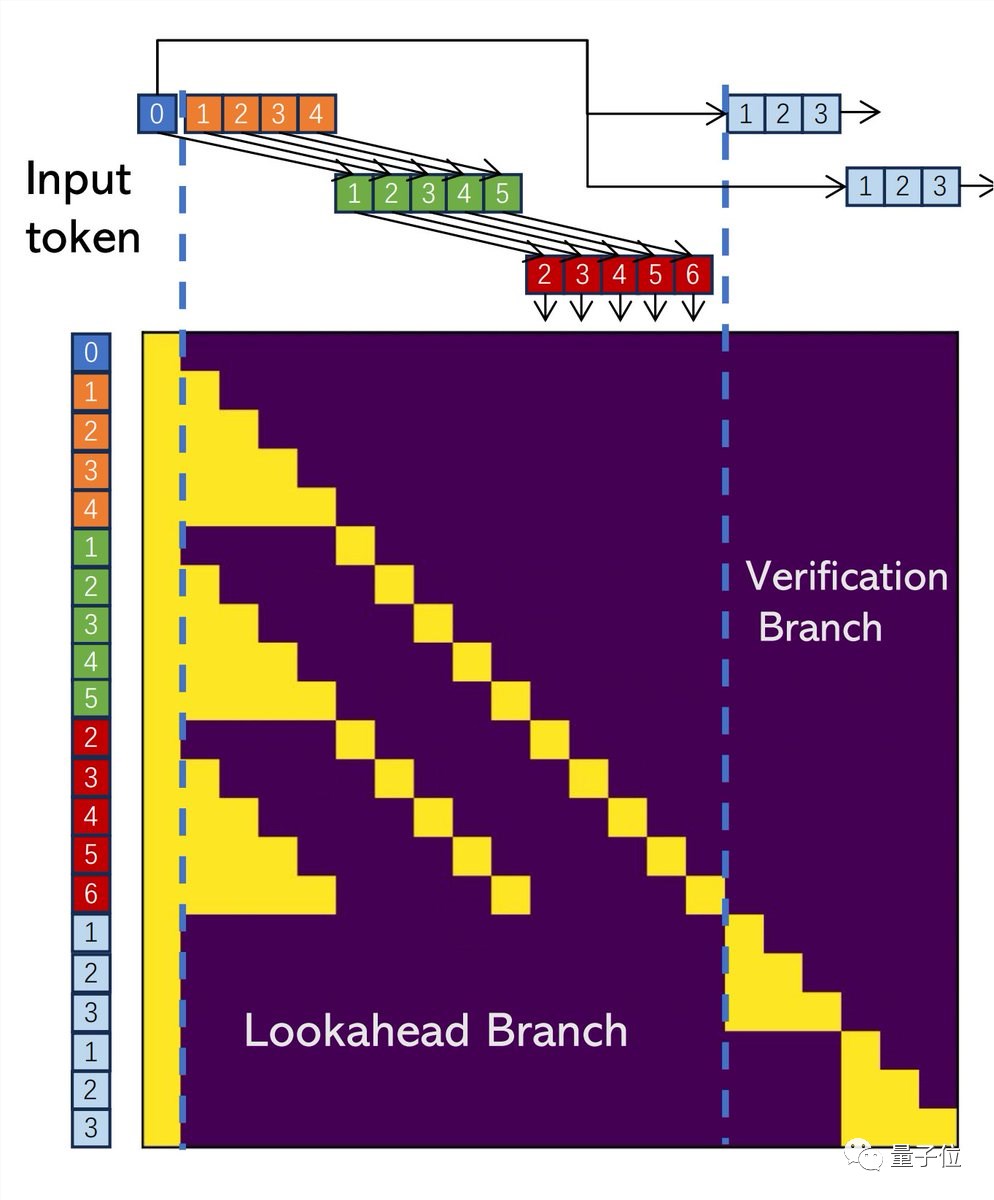
4、前向解码无需外部源即可立即生成并验证非常多的n-grams。这虽然增加了步骤的成本,但也提高了接受更长n-grams可能性。
换句话说,前向解码允许用更多的触发器来减少延迟。
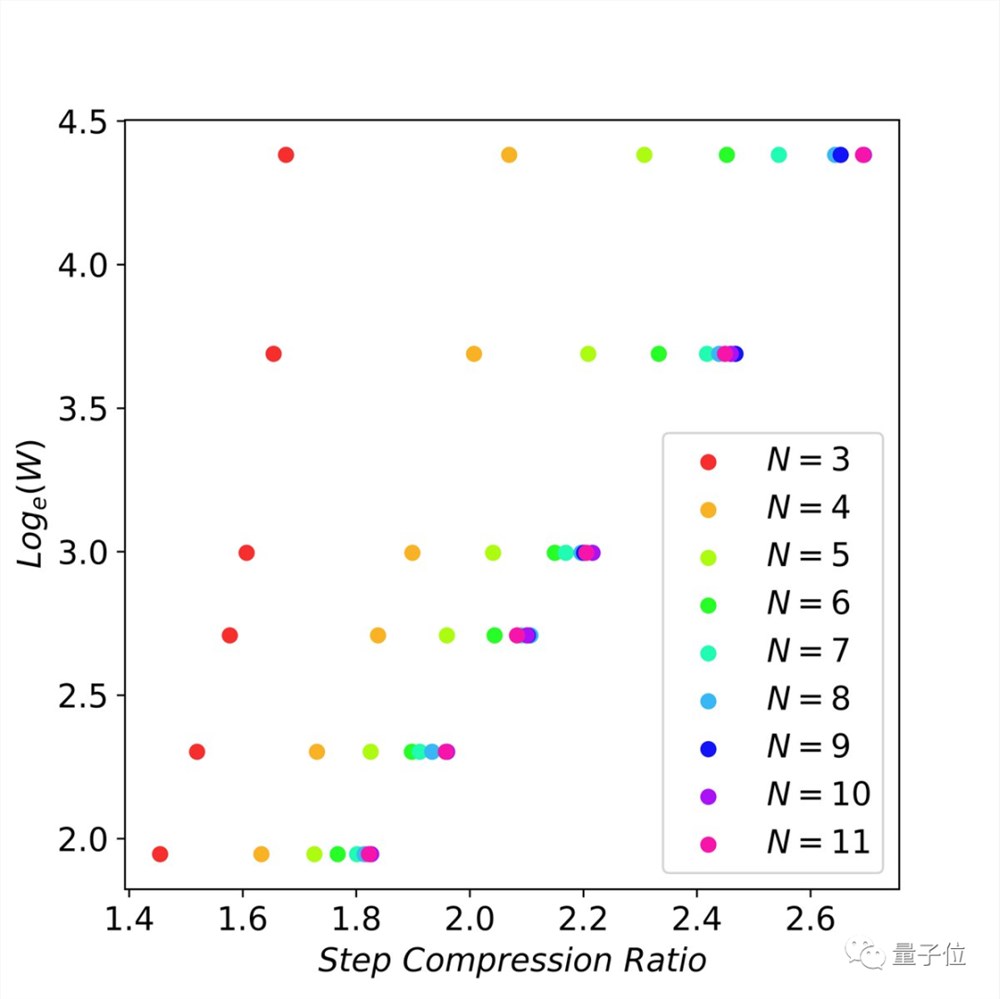
5、作者检查了flops vs 延迟减少之间的缩放行为,并找到了缩放法则:
当n-grams足够大时(比如11-gram),以指数方式增加未来的token猜测(即窗口大小)可以线性减少解码步骤数。
作者介绍
本方法作者一共4位,全部来自小羊驼团队。

其中有两位华人:
傅奕超以及张昊,后者博士毕业于CMU,硕士毕业于上交大,现在是加州大学圣地亚哥分校助理教授。
参考链接:
[1]https://twitter.com/lmsysorg/status/1727056892671950887
[2]https://lmsys.org/blog/2023-11-21-lookahead-decoding/
[3]https://github.com/hao-ai-lab/LookaheadDecoding
- 0000
- 0000
- 0000
- 0000
- 0000